熱伝導率測定法について


　熱伝導率kは定常熱流法で測定した。試料周辺の概略図をFig.1に示す。細長い試料はその一端をヘリウム冷凍機のcold head上の銅ブロックにインジウム半田を用いて熱的に接触させる。他端には熱源となる金属皮膜チッフﾟ抵抗ヒーター1kΩを絶縁ワニスGE7031を用いて接着する。試料上の2カ所P1、P2の温度測定はAu + 0.07at%Fe（AuFe）− クロメル熱電対（直径0.076mm）を用いて測定する。いずれの熱電対接点も、GE7031ワニスで試料上に接着し、熱電対素線の熱伝導による試料と外部との熱の流入･流出を軽減するためにcold headでサーマル･アンカーをとってある。輻射伝熱による損失を防ぐために、試料周辺にはニッケルめっきを施した銅製の輻射シールドを2重に配置した。また雰囲気ガスによる対流伝熱による熱損失を無くすために、測定室内は油拡散ポンプを用いて1×10−6Torr程度の真空度に維持した。測定はまず試料の温度を安定させ、抵抗ヒーターに定常電流を流して試料に熱流Q[W]を与え、その時に２点、P1、P2の温度差dT[K]を測定する。熱伝導率kは

k[W/cmK]=(QS)/(dTL) (1)

で計算することができる。ただしS[cm2]は試料の断面積、L[cm]は２点P1、P2の距離である。測定は、パソコンとデジタルマルチメータ（DMM）、電流源、スキャナー等をGPIBケーブルで接続し、自動計測を行っている。


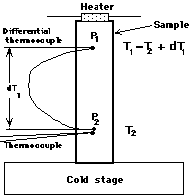Fig.1:試料周辺の概略図

参考文献：
・M. Ikebe, H. Fujishiro, T. Naito and K. Noto, Simultaneous Measurement of Thermal Diffusivity and Conductivity Applied to Bi-2223 Ceramic Superconductors, J. Phys. Soc. Jpn. 63, 3107-3114 (1994).
・保原夏朗、松川倫明、松浦伸悌、藤代博之、能登宏七、ヘリウム冷凍機を用いた熱伝導率の完全自動測定、低温工学　28, 688-692 (1993).

熱拡散率測定法について

・熱拡散率αは、Fig.1の熱伝導率測定と同一セッティングで任意加熱法によって測定した。熱源であるヒーターに数秒間の電流パルスを印加し、試料にパルス状の熱流を与える。この熱流が輻射および対流伝熱による熱損失がなく、coldhead側に一方向に流れ込むと仮定できるとき、熱の拡散は次に示す一次元の熱拡散方程式に従う。

∂T/∂t=α(∂2T/∂x2) (2)

ここで、αは熱拡散率、xは距離、T(x,t)は距離x、時刻tでの温度である。熱流方向を＋x軸にとりP1を原点（x=0）として、熱パルスを与えた後のP1およびP2（x=L）の過渡的な温度変化T1(t) 、T2(t) を毎秒約3.1回のサンプリング速度で測定し、記録する。ヒーターに与える電流パルスは、T1(t) の温度変化ΔT1が1.5＜ΔT1＜2.5Kの範囲になるように調節した。(2)式で与えられる熱拡散方程式を適切な境界条件のもとで解くことで熱拡散率αを決定できる。本研究では、T(x,0)を初期条件、T1(t) 及びcold headの温度（設定温度で一定値）を境界条件として、x=Lでの理論温度T2'(t) を様々なαの値について数値的に計算し、実験値T2(t) との平均自乗誤差を評価することで最適な熱拡散率αを決定した。一連の数値計算は、パソコンを用いて行った。

・熱拡散方程式のような偏微分方程式を数値的に解く方法としては、差分近似解法が広く一般的に用いられている。差分近似の方法には大別して、陽解法と陰解法の二種類があるが、本研究では近似解の収束性及び安定性を考慮して、Crank−Nicolsonの陰解法を用いた。近似差分方程式を作り、こてに境界条件を代入すると、(2)式で与えられる熱拡散方程式は、線形代数連立方程式に書き換えることができる。この連立方程式をGaussの消去法を用いて解くことで、任意の時刻t及び任意の距離xにおける温度を計算することが可能である。

・熱拡散率αを決定するまでの過程をステンレス標準試料(SRM1460)の150Kの測定結果を用いて以下に示す。まず、ヒーターに9mA、5秒の電流パルスを印加したときのT1(t) 、T2(t) の測定データをFig.2に示す。T1(t)とcold headの温度を境界条件として種々のαについてT2'(t) を計算し、T2(t) にフィッティングする様子をFig.3に示す。本研究では、温度応答がピークを迎えるまでのデータを用いてその立ち上がり10%〜90%のデータ点について平均自乗誤差を評価した。αと誤差の自乗平均の関係をFig.4に示す。この図のように平均自乗誤差の最小値を与えるαを決定した。

・ステンレス標準試料（SRM1460）、高純度銅（6N）およびパイレックスガラス（Corning　#7740）の熱拡散率の測定結果から、本研究の方法で測定した熱拡散率は、0.5〜200mm2/secのオーダーで絶対精度10%以内で測定出来ることがわかった。



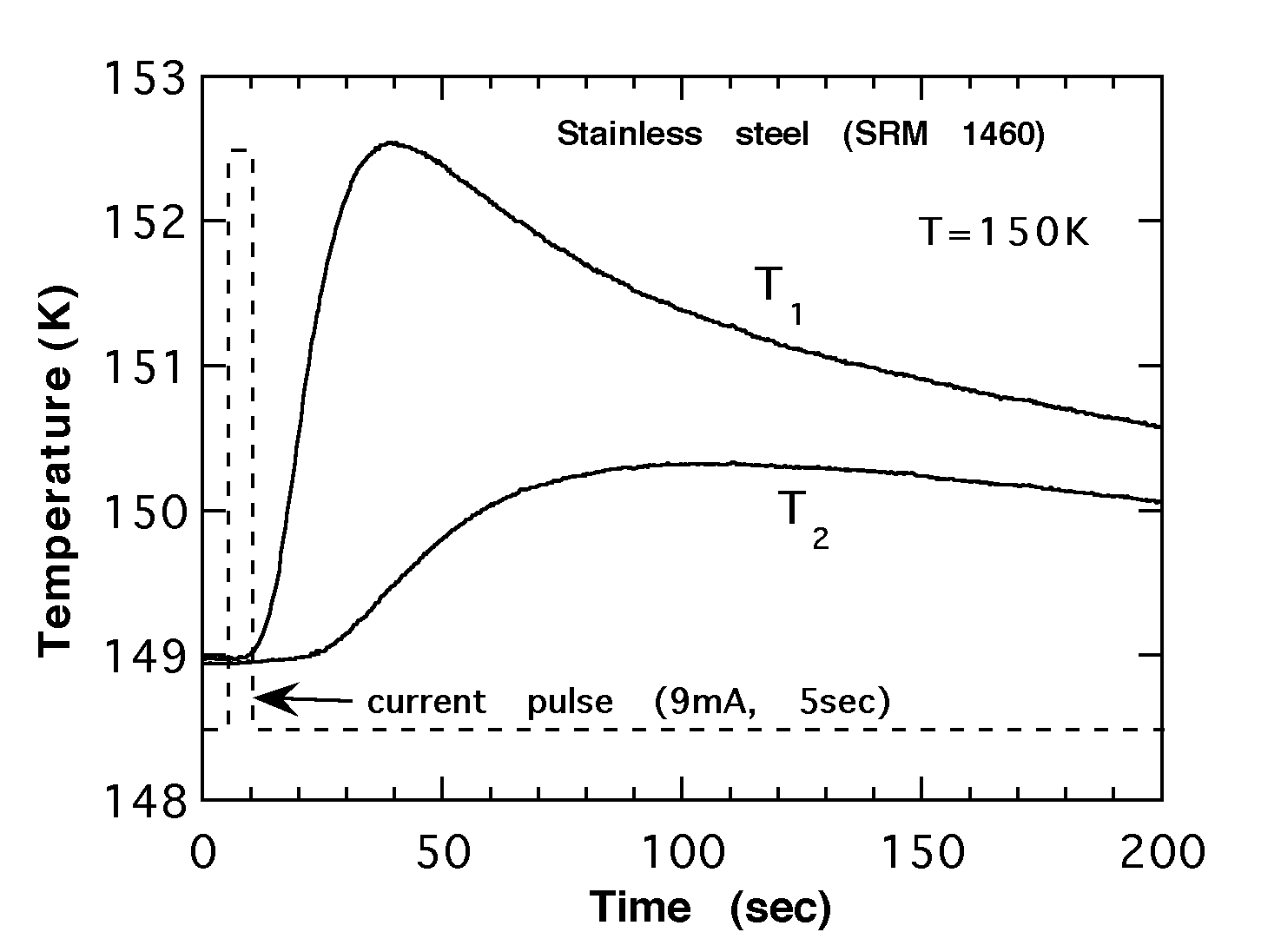
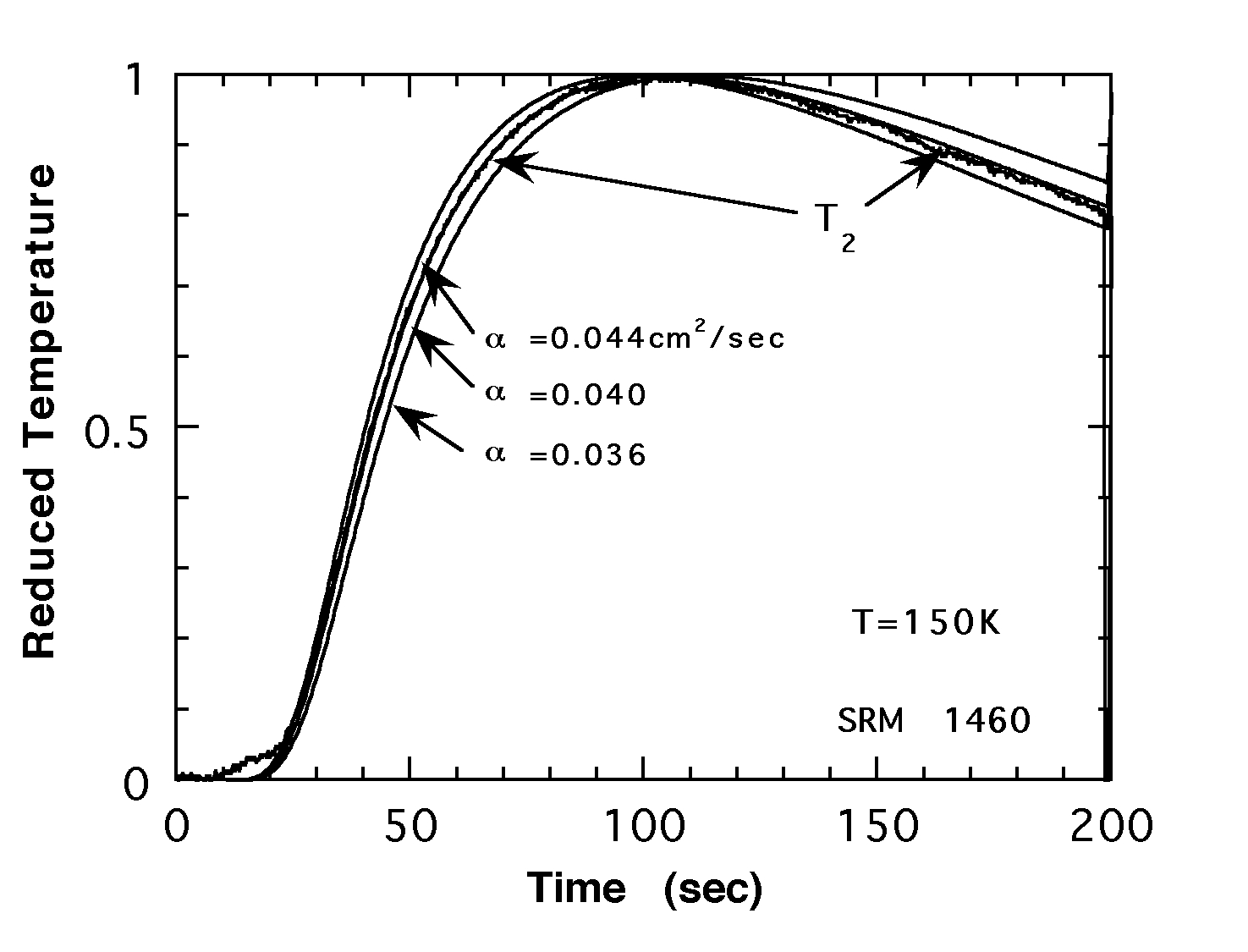
左から、Fig,2:(SRM1460)の150KのT1(t) 、T2(t) Fig.3: T2'(t) とT2(t) のフィッティングの様子


Fig.4:αと誤差の自乗平均の関係

参考文献：
・M. Ikebe, H. Fujishiro, T. Naito and K. Noto, Simultaneous Measurement of Thermal Diffusivity and Conductivity Applied to Bi-2223 Ceramic Superconductors, J. Phys. Soc. Jpn. 63, 3107-3114 (1994).
・藤代博之、池部　学、内藤智之、能登宏七、低温における熱拡散率と熱伝導率の同一セッティング測定、低温工学　28, 533-539 (1993).

磁場中熱物性測定装置について


　2000年より岩手県地域結集型共同研究事業「生活・地域への磁気活用技術の開発」プロジェクトに参画し、磁場中熱物性測定装置の開発を行っている。
測定項目は、熱伝導率、熱拡散率、比熱、熱起電力、熱膨張、音速であり、4〜300Kの温度範囲で、0〜10Tの磁場中での測定を完全自動で行うことができる。この装置を用いて、酸化物超伝導材料（単結晶、バルク溶融体、線材）および関連材料（金属材料、FRP、エポキシ樹脂など）の測定を行っており、最終的にはこれらの材料の熱物性データベースの構築を目指している。



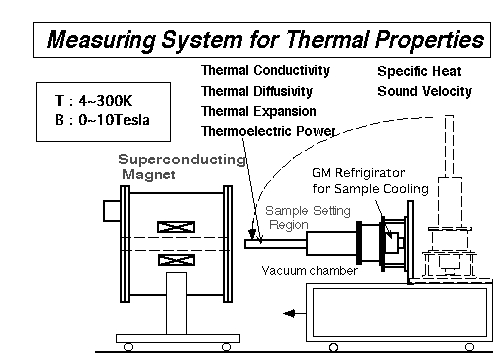
Fig.5:試料周辺の概略図

接触熱抵抗の測定方法について


　低温に用いる機器や装置の製作または低温を用いる実験において、異種物質を機械的に接続することは（例えば、クライオスタットの製作や超伝導体・常伝導体接続など）頻繁に行われる。通常はハンダ付け、接着、機械的圧着等の方法が用いられるが、界面における接触熱抵抗Rcが問題になる場合が多い。異種物質間の接続における接触熱抵抗Rcは一般に温度の低下とともに増大するが、接触表面の平坦度、介在物の厚さ、接続方法等により変化し、一義的に決定できる物理量ではないため、装置設計の場合も理想的にRc=0としたり経験的な値を用いるなど、極低温におけるKapitza界面抵抗に関する研究の他は定量的な議論はほとんど行われていないのが現状である。本研究グループでは、非定常法（３点同時測定法）および定常法（定義に基づいた測定）による接触熱抵抗Rcの測定法を開発した。

（１）非定常法（３点同時測定法）による接触熱抵抗Rcの算出
　本研究グループでは、低温における熱拡散率aの測定を、Fig.1のようなセットアップ（２点法）で行ってきた。この場合には試料とCu Blockの間の接触熱抵抗はゼロとして解析してきた。また熱伝導率kと熱拡散率aの間にはk=Caという関係が成立し、kとaの測定から比熱Cが算出できる。高温ではデバイの比熱式に一致した比熱の振る舞いを示すが、低温（特に50K以下）ではデバイの比熱よりも大きく比熱を見積もってしまう。この原因は、低温で接触熱抵抗Rcが無視出来なくなり、熱拡散率aを実際よりも小さく見積もっているためと考えた。このことを検証するために、Fig.6に示す任意加熱法における3点同時測定法を提案し検討を行ってきた。２点法との相違点は、試料上の3カ所の温度測定を行うことである。Fig.7に解析のフローチャートを示す。３点同時測定法により固体と固体の接続により生じる接触熱抵抗率を求め、同時に接触熱抵抗率を考慮した熱拡散率測定を行う方法をを完成させた。



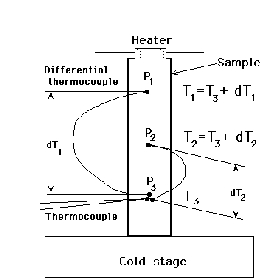
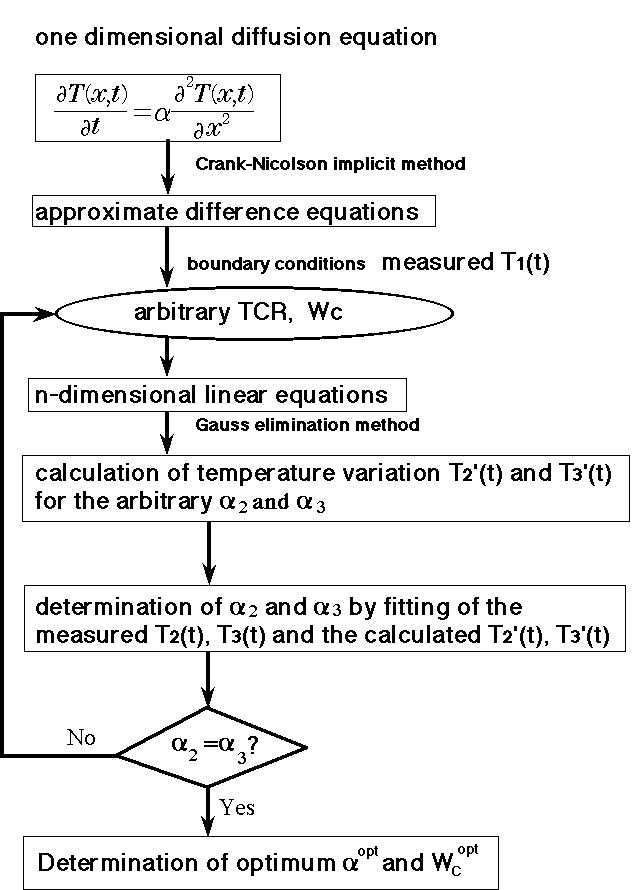
Fig.6:3点同時測定法のセットアップFig.7:解析のフローチャート


（２）定常法による接触熱抵抗Rcの測定
　　２つの物質の界面を熱流Qが通過するとき、界面における接触熱抵抗Rcは界面における温度の不連続がdTの場合Rc=dT/Q (K/W)と定義される。本研究では酸化物超伝導体YBCOと金属Cuの接続を考え、Fig.8に示すように熱流Qを与えた後のYBCO上の熱流方向に３点の温度とCuの温度をモニタし、界面におけるにおける温度の不連続dTを熱流Qを変化させた実験から平均して求めた。また同一のセットアップでYBCOの熱伝導率k、および熱パルス印加後の温度の時間応答から熱拡散率αを測定した。YBCOとCuの接続は平面接触とし、接続方法はインジウム半田付け、銀ペースト接着およびGEワニス接着により行った。測定する設定温度に点P1, P2, P3での温度T1, T2, T3を安定させ、Heaterから一定電力Q[W]（=I2R: ただしI[A]はヒータ電流、R[ohm]はヒータ抵抗]を加え、試料の温度分布が一定になったところで温度差dT1, dT2, dT3を記録する。Heater電力Qを加えたことにより上昇した温度と端子間距離からFig.8のように作図し、試料とCu Blockの境界面の温度の飛躍ΔTを求め次の式で接触熱抵抗Rcを算出する。 　Fig.9に３種類の異なる接続をした場合の接触熱抵抗Rcの温度依存性を示す。いずれの接続においてもRcは温度の低下とともに増大し、特に50K以下で急激に大きくなる。Rcの絶対値はGEワニス接着、インジウム半田付け、銀ペースト接着の順に小さくなり、 GEワニス接着は他の２つの方法に比べ１桁以上Rcが大きいことが分かった。熱伝導率測定のような定常熱流による測定の場合には、接触熱抵抗の存在は測定結果に影響を与えないが、熱拡散率や比熱測定のような非定常熱流測定の場合には、界面での熱流の停滞現象のため測定結果に大きく影響する。特に低温ではRcの低減とRcを考慮に入れた解析が重要になる。



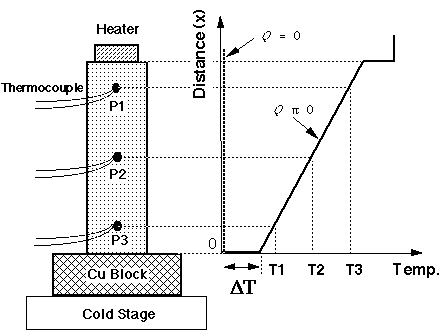
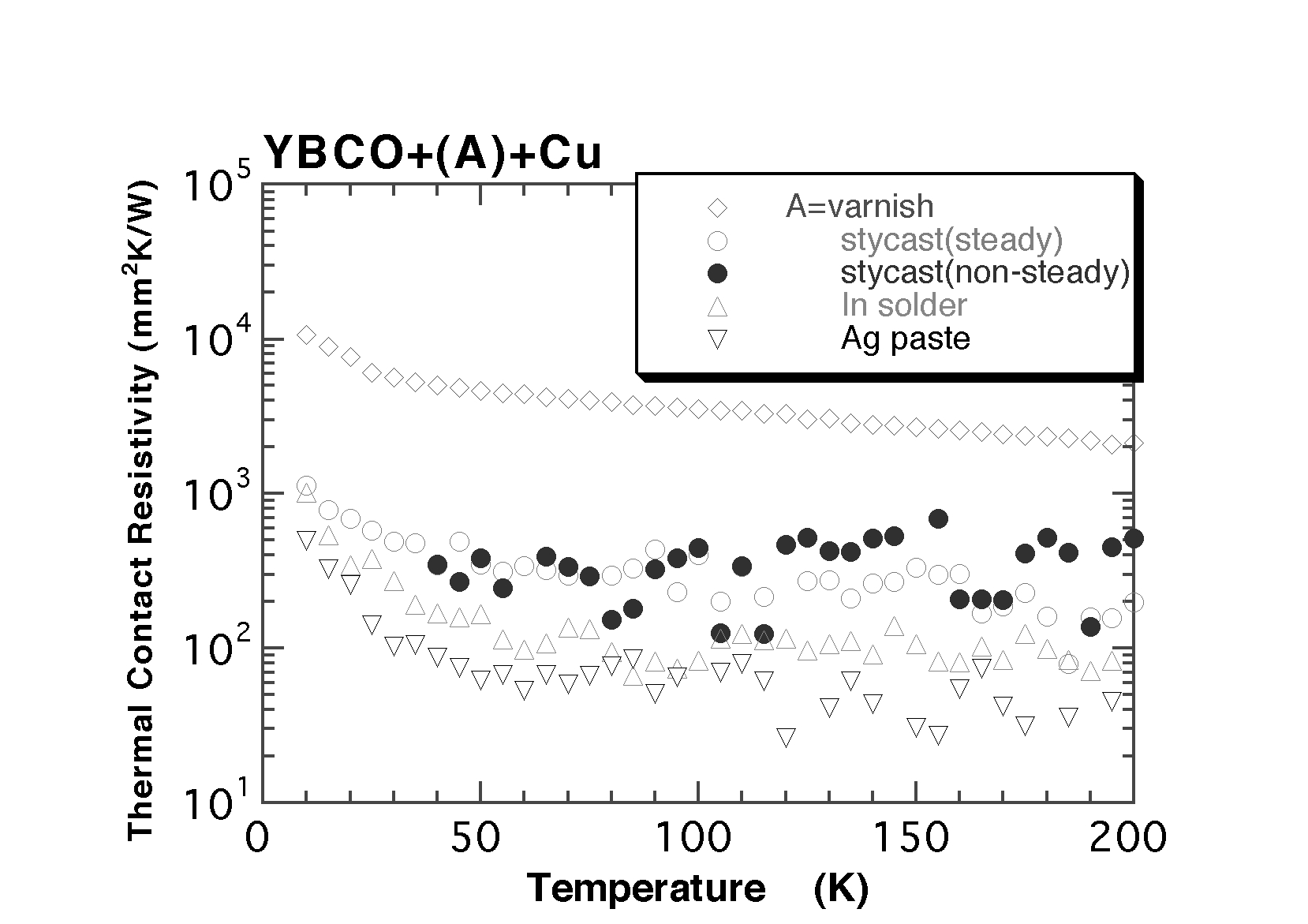
Fig.8:定常法による接触熱抵抗Rcの測定のセットアップ：Fig.9:３種類の異なる接続をした場合の接触熱抵抗Rcの温度依存性

参考文献：
・H. Fujishiro, M. Ikebe, K. Nakasato and T. Naito, Proposal of Three Terminal Method for Low Temperature Thermal Diffusivity Measurement, Czech. J. Phys. 46 Suppl. S5, 2761-2762 (1996).

・接触熱抵抗論文2001

２次元熱伝導率同時測定法について


　一般に、低温における等方的な物質の熱伝導率は定常熱流法により測定されるが、異方性を有する物質に対する異方的熱伝導率は、原理的には各々の方向に細長い試料を用いて同様に定常熱流法によって測定可能である。しかし、例えば酸化物超伝導体単結晶では、ab面内の熱伝導率kabは定常熱流法で比較的容易に測定できるが、c軸方向の熱伝導率kcはc軸方向に厚い試料の作製が困難であるため測定が難しく、SやLの測定誤差の影響が大きくなる。本研究グループでは、２次元的な異方性を持つ物質の異方的な熱伝導率を、同一セッティングでしかも一度の測定で求める新しい測定法を開発した。
Fig,10に本研究で用いた試料のセッティングの概観を示す。ヒータと熱浴を図のように配置して熱流を斜めに試料に加えた後の試料上のP1, P2, P3の温度上昇と、熱流の数値シュミレーションから求めた温度上昇の比較から２次元的な熱伝導率を求めることができることを実証した。


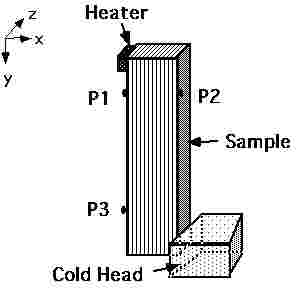Fig.10:２次元熱伝導測定のための試料周辺の概略図

参考文献：

・H. Fujishiro, T. Okamoto,M. Ikebe and K. Hirose "A New Method for Simultaneous Determination of Anisotropic Thermal Conductivities Based on Two-Dimensional Analyses", Jpn. J. Appl. Phys. 40, pp388-392, 2000
・H. Fujishiro, M. Ikebe, K. Nakasato and T. Naito, "Proposal of Three Terminal Method for Low Temperature Thermal Diffusivity Measurement", Czech. J. Phys. 46 Suppl. S5, pp.2761-2762, 1996